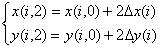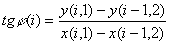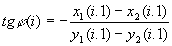ГРАВИТАЦИОННАЯ МЕТРИКА ПРОСТРАНСТВА-ВРЕМЕНИ
ПРОЕКТ
НОВАЯ ГРАВИТАЦИЯ
можно также посмотреть Обсуждение на Scientific.ru
В сжатом виде смотрите Физическая интерпретация решения Шварцшильда
ГРАВИТАЦИОННАЯ МЕТРИКА
ГРИБАНОВСКИЙ Е.К.
Предложен физический процесс, соответствующий идее искривления геометрии пространства-времени Эйнштейна для объяснения Гравитации. Получение основных результатов стало возможным за счёт последовательного применения принципа эквивалентности Эйнштейна, приводящего к понятию динамичной метрики. Рассматриваются четыре выделенные системы координат в центрально-симметричной области тяготения, приведены формулы перехода между ними. Разъяснён физический смысл решения Шварцшильда. Сделан расчёт результатов опыта Паунда-Ребки, а также отклонения траектории светового луча Солнцем, без привлечения понятия гравитационного поля, совпавшие с экспериментом. Обнаружен эффект отклонения луча света от центра гравитации вблизи перигелия.
- I -
Целью работы является показать физический смысл того искривления геометрии пространства-времени, которое было введено А.Эйнштейном для объяснения Гравитации.
ОТО Эйнштейна остаётся и сейчас лучшим образцом человеческого разума.Созданная почти 80 лет назад, ОТО лишь в последнее время стала применяться в практической деятельности человека (расчёт траектории межпланетных станций, спутниковые навигационные системы).Нет поводов сомневаться в корректности и точности ОТО и Теории гравитации в её рамках.
Тем не менее не прекращаются попытки разработки альтернативных теорий гравитации,начиная от Ми и Вейля и заканчивая А.Логуновым (1).Попытки эти закончились ничем, хотя побудительные мотивы для работ такого рода имеются.
В первую очередь это математический аппарат, применённый А.Эйнштейном - М Гроссманом. Как следствие - Теория гравитации получилась локальной. Практически все формулы рассматривают "искажение геометрии" в точке. Что это за "искажения", какой физический смысл они несут, остаётся неизвестным. Декларативно вводятся коэффициенты g(i,k) [2-(82.1)], полезные математически, но не обоснованные физически. Как следствие, решение Шварцшильда, как и других решений, дающих общую картину "искажения геометрии", выводится не из формулы уравнения гравитационного поля Эйнштейна [3-(401a)], а из формулы для инварианта длины [3-(100.1)]. Тем не менее, исходная позиция как для изучения ОТО, так и для попыток дальнейшего развития ОТО и Теории гравитации в её рамках, начинается именно с рассмотрения геометрии в точке, без ясного понимания физического содержания упомянутого "искривления".
Некорректность такого подхода можно показать на примере оценки величины вышеупомянутых функций пространственных координат g(i,k) . Неявно подразумевалось, что бесконечно малым дифференциалам соответствуют бесконечно малые величины g(i,k) .Об этом писал сам Эйнштейн: "Однако позднее Леви-Чивитта правильно указал на то, что элементом теории, позволяющим устранять инерциальную систему, является, собственно говоря, поле бесконечно малых смещений.... "[7-стр 855]. И далее "Этот недостаток исправляется введением поля бесконечно малых смещений. Оно заменяет инерциальную систему постольку, поскольку позволяет проводить сравнение векторов в бесконечно близких точках"[7-стр856].
Как показывается ниже, эти " бесконечно малые смещения" составляют на поверхности Земли величину 11,2км/сек.
ОТО описывает гравитацию в терминах метрики в точке, поэтому сопоставление результатов, полученных для двух удаленных точек, затруднено, так же как и результаты для одной точки, полученные в разных системах координат. Например, Шмутцер Э. прямо пишет: "Поскольку наше реальное пространство-время обладает кривизной....и обращаться к координатам Галилея как к решающей инстанции при проверке истинности высказываний относительно длины и времени, вообще говоря, невозможно, сравнение физических результатов, полученных в различных системах координат, оказывается делом чрезвычайно трудным . Нередко доказательство тождественности двух решений поля Эйнштейна, полученных в различных системах координат, само по себе становится темой важного научного исследования".[5-125]. И далее: "...несмотря на то, что точных математических решений более чем достаточно, лишь немногие из них получили убедительное физическое истолкование.... Число нетривиальных точных решений, вполне понятных с точки зрения физики, весьма невелико." [5-140]. С ним соглашается Владимиров Ю. : "В настоящее время известно большое число точных решений уравнений Эйнштейна, однако лишь некоторые из них получили ясное физическое истолкование ..... " [6-113].
Для иллюстрации вышеприведённых цитат приведу пример с решением Шварцшильда. Оно выведено в 16 году прошлого века, однако понимания механизма его действия нет до сих пор. Когда пытаются применить его к расчётам, происходят непонятные вещи. Делают разложение в ряд и ограничиваются первым значащим членом [5-152] для определения замедления времени. Для определения "красного смещения" Ландау прибегает к эйконалу, при этом делает оговорку о слабости гравитационного поля и получает приближенную формулу [2-(88,7)], причём у него откуда ни возьмись появляется понятие потенциала гравитационного поля, то есть от позиций геометрического подхода к гравитации как бы незаметно перешли к понятию силового гравитационного поля. Это излишне, поскольку в решении Шварцшильда уже содержится всё для получения этого самого "красного смещения", как, впрочем, и для "гравитационного замедления времени", причём без каких-либо приближений и выхода за рамки геометрической гравитации. Это показано ниже в разделе IV для расчёта результатов опыта Паунда-Ребки.
Подчеркну ещё раз: для понимания Гравитации нет необходимости привлекать понятие силового гравитационного поля.
Ниже рассмотрены четыре выделенных системы координат центрально-симметричной области тяготения, приведены формулы перехода от одной системы к другой. Область тяготения рассматривается в целом, поэтому не возникает трудностей в сопоставлении решений гравитации как между точками, так и решений в одной точке в разных системах координат.
Моё убеждение в необходимости пересмотра механизма гравитации в рамках ОТО возникло после внимательного рассмотрения формулы, приведенной в Паули [3-233]
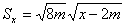 (1)
(1)
где m - масса, x - расстояние от центра.
Когда я, в свою очередь, вывел эту формулу, она меня поразила, и я отнёсся к ней как к
ошибочной
.
Однако позже я обнаружил подобные формулы у Паули [3-233], и ещё по крайней мере у двух авторов.
Эта формула была получена мною в предположении, что наша Вселенная есть трехмерная поверхность раздела в четырехмерном мире. При этом
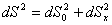 (2)
(2)
где dS - реальный интервал в присутствии гравитационного поля
dS0 - интервал в отсутствии гравитационного поля,
dSX - составляющая в четвертом измерении, определяющая гравитационное поле.
Как оказалось позднее, мои построения были неверны, тем не менее формула получена в рамках Теории гравитации, и не только мною, и должна соответствовать нашему Миру. Но для неё не выполняются граничные условия - при устремлени Х к бесконечности она не соответствует плоскому Галилееву пространству,
искажение метрики стремится к бесконечности, чего на самом деле нет, - значит, возникает вопрос о корректности всей ОТО.
Поэтому, поскольку формула (1) соответствует ОТО, то остаются две возможности. Первая - пересмотр основополагающей формулы [3-(421a)] - или, вернее, порождающей ее формулы [3-(410)], и второй - наше понимание формулы (1).
Дальнейшая работа проходила с переменным успехом над обеими возможностями, и, к некоторому изумлению, привела к положительным результатам на обоих направлениях.
В дальнейшем будет рассматриваться центрально-симметричная область тяготения, поскольку любые другие области тяготения могут быть представлены как суперпозиция элементарных центрально-симметричных областей.
- II -
Вступление к изложению геометрии пространства - времени в присутствии гравитации уже имеется. Это работы Эйнштейна, его принцип эквивалентности. Приведем его в изложении Паули: "Для бесконечно малой области четырехмерного мира (т.е. для области столь малой, что пространственно-временными изменениями силы тяжести в ней можно пренебречь) всегда существует такая система координат K0(X1,X2,X3,X4), в которой сила тяжести не влияет ни на движение материальной точки, ни на любые другие физические процессы. Коротко говоря, в бесконечно малой области мира любое поле тяготения может быть уничтожено с помощью преобразования координат. Местная координатная система K0 может быть мыслима в виде свободно падающего, достаточно малого ящика, на который не действуют никакие внешние силы, кроме силы поля тяжести, в котором он свободно падает".[3-205].
Это так называемый лифт Эйнштейна.
Еще раз повторю принцип эквивалентности другими словами. Если материальная точка находится в свободном падении, то окружающее ее пространство неотличимо от пространства вдали от источника гравитации.
Рассмотрим подобную материальную точку вместе с ее окрестностью, находящуюся на расстоянии r0 от центра источника гравитации. Через время 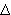 t эта точка переместится на расстояние
t эта точка переместится на расстояние  r0 к центру. Поскольку поле центрально-симметричное, то такие же материальные точки, расположенные на r0 от центра, образуют сферу и все они переместятся к центру через время
r0 к центру. Поскольку поле центрально-симметричное, то такие же материальные точки, расположенные на r0 от центра, образуют сферу и все они переместятся к центру через время 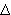 t на расстояние
t на расстояние 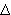 r0.
r0.
На место этих материальных точек переместятся другие, находившиеся дальше на расстоянии r0+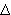 r-1.
r-1.
Таким образом, все пространство вокруг источника гравитации можно расслоить на концентрические сферы, которые через время 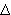 t сменяют друг друга, устремляясь к центру.
t сменяют друг друга, устремляясь к центру.
Любой физический процесс, происходящий между сферами (или на них) будет неотличим от такого же процесса вне действия гравитации, если местная система координат этого физического процесса будет привязана к движению этих падающих концентрических сфер.
Вообще говоря, принципу Эйнштейна будут удовлетворять любые скорости согласованного движения этих концентричных сфер, но лишь один набор скоростей будет удовлетворять граничному условию - равенство нулю на бесконечности, а именно в соответствии с формулой второй космической скорости.
Эта формула давно известна
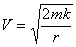 (3)
(3)
где k - гравитационная постоянная, m - масса центра гравитации, r - расстояние от центра гравитации.
Формула для ускорения падающей системы также давно известна
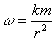 (4)
(4)
Впрочем, (4) легко получается из (3).
Формула (3) дает поле скоростей, полностью определяющее область гравитации.
Поясню этот тезис. Исходная идея Эйнштейна о том, что причиной Гравитации является искривление геометрии, реализуется в виде подвижной метрики, или падения пространства, или динамичной геометрии,или смещение локальной системы отсчёта, или падающая система координат. Может быть, приживётся название Эйнштейновская система координат, или Эйнштейновская метрика.
Понятие новое, поэтому термин, удовлетворяющий всех, подобрать трудно.
Формула (3) показывает, насколько проста Гравитация: в неё входит только две переменных - направление и скорость сдвига (для данной массы в центре тяготения).
- III -
Известно, какое большое значение имеет правильный выбор точки отсчета, начала координат, для упрощения теории или решения физической задачи в ее рамках.
Не надо ходить далеко - подобный пример находится внутри теории тяготения, а именно задачи движения планет. В геоцентрической системе мира Птолемея точкой отсчета является Земля. Это было чрезвычайно неудобно, для астрономии целостной картины движения планет не было - достаточно вспомнить видимые петли в движении внешних планет.
Предложенная Коперником точка отсчета - Солнце - резко упростила задачу, и вскоре была создана теория тяготения Ньютона. Нельзя сказать, что учение Птолемея неверно - все зависит от последующей сложности решения физической задачи в результате выбора точки отсчета: Земля или Солнце. Именно в этом содержится выбор коперниковской системы отсчета, и птолемеева система мира с такими красивыми терминами, как эпицикл, деферент, небесная сфера: осталась только в истории.
В области действия гравитации можно отметить несколько выделенных систем отсчета. Первая - мировая система координат. Именно относительно этой системы приводятся результаты вычислений движения планет в солнечной системе или спутников вокруг Земли при рассмотрении земного тяготения. Относительно этой системы даны и результаты в ОТО - например, решение Шварцшильда или Керра. Вслед за Эйнштейном будем называть эту систему отсчета галилеевой.
Вторая выделенная система - это обычная традиционная система на поверхности небесных тел, то есть неподвижных относительно центра тяготения, например, на Земле,- относительно галилеевой системы они также неподвижны. Решением уравнения Эйнштейна для этого случая - центрально-симметричного тяготения - является решение Шварцшильда. Главная его особенность - неизменность расстояния до центра, а проявления гравитации объясняются искажением метрики пространства - времени.
Мои усердные поиски - как же эти искажения проявляются и какие это искажения - обнаружили лишь невнятные утверждения, что эти искажения метрики якобы проявляются как силовые поля. И еще замедление времени, также рассматриваемое как якобы искажение метрики. Именно наличием таких "искажений" шварцшильдовская система координат отличается от галилеевой. Переход от одной системы к другой дается решением Шварцшильда, которое будет рассмотрено позднее.
Именно неочевидность механизма искажений метрики привела к следующей, - третьей - выделенной системе координат, развиваемой в данной работе. Это падающая, или Эйнштейновская, система координат. Связь ее с галилеевой системой дается формулой (3).
При переходе к декартовой системе отсчета (3) будет:
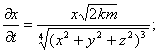
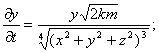
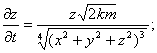 (5)
(5)
Идея о подвижности пространства не нова. По-видимому, впервые об этом заявлено в работе Фридмана о модели Вселенной. В ней меняются расстояния между точками при расширении Вселенной, то есть они подвижны. Сценарий "Большого взрыва" также развивает идею подвижного пространства (см., например, [7]). Как оказывается, пространство движется не только в масштабах Вселенной: ускоренное движение пространства есть форма существования гравитации .
Кстати, скорость смещения падающей системы координат (или Эйнштейновской системы координат) сквозь поверхность Земли легко узнать, - она в точности равна второй космической скорости, то есть около 11,2 км/сек - именно такую скорость приобретает любое тело вместе с окружающим его пространством, падающее из бесконечности на Землю. Сквозь нас сверху вниз смещается пространство, падает с ускорением, а поскольку все физические процессы между телами, молекулами, атомами, электронами и ядром атома происходят через падающую систему, то это каждая точка, неподвижная относительно поверхности Земли, движется с ускорением вверх относительно окружающего ее пространства.
В каждый момент времени от точки, неподвижной в шварцшильдовской системе, пространство в ее окрестности смещается вниз в соответствии с (3).
- IV -
Рассмотрим связь падающей системы с шварцшильдовской. Приведем формулу решения Шварцшильда в форме [2-(100.14)].
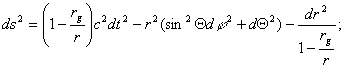 (6)
(6)
где
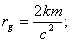
если
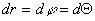 =0,
=0,
то
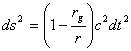
раскроем скобки и подставим значение для rg
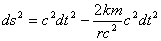 или
или 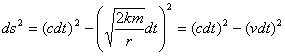 (7)
(7)
Вспоминая определение интервала, видим, что ds является суммой двух ортогональных величин, первое из которых интервал времени, а второе - смещение пространства за тот же самый интервал времени, определяемый (3).
Первое слагаемое в (7) показывает, что темп времени падающей и галилеевой систем совпадают между собой. В то же время точки в шварцшильдовской системе имеют скорость относительно падающей системы, определяемое (3), и испытывают банальное замедление времени по формуле преобразования Лоренца. [2-(3.1)]
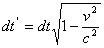 где
где 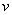 берется из (3)
берется из (3)
Проверим это. Возьмём две неподвижные точки, разнесённые по высоте. Каждая такая точка будет иметь свою скорость относительно падающей системы и, значит, своё Лоренцево замедление времени.
Предположим,что из одной точки в другую излучается точно известная частота (например, при переходе ядра атома из одного состояния в другое). Для удалённого наблюдателя эта частота будет смещена в красную сторону, поскольку точка излучения испытывает Лоренцево замедление времени. Обычно это явление называют "гравитационное замедление времени" и "гравитационный сдвиг частоты, или красное смещение".
В другой точке эта частота будет приниматься с учётом своего замедления времени. Сдвиг частоты будет зависеть от относительной разности скоростей этих точек в падающей системе. И этот опыт уже проведён.
Одним из наиболее точных (~1%) опытов по гравитационному сдвигу частоты излучения является
опыт Паунда-Ребки
( Pound–Rebka )
на основе применения эффекта Мёссбауэра [5-151]. При разности высот 22,5м сдвиг частоты 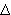
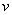 равен
равен
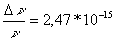 [5-(3.29)]
[5-(3.29)]
Однако этот так называемый "гравитационный сдвиг частоты излучения" имеет в своей основе гораздо более прозаическое замедление времени [3-(17а)], см. также [3-(8)].
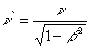 где
где 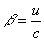 , u - скорость.
, u - скорость.
Возьмём производную по u:
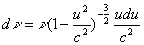 или
или 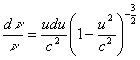 (8)
(8)
Получили относительный сдвиг частоты между двумя движущимися объектами, имеющими скорости u и u+du.
Возьмём производную по r для (3), предварительно заменив v на u.
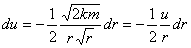
Подставив r = 6.37*106 м, u = 11.2*103 м/сек (для поверхности Земли), dr = 22.5 м. Получим
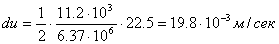
это разность скоростей падения пространства для точек, разнесенных по высоте на 22,5м.
Подставив числовые данные в (8) получим
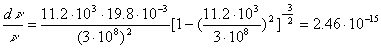
Получили удовлетворительное совпадение с экспериментом [5-(3.29)].
Ещё раз подчеркну, что это совпадение теоретического расчёта и опыта получено в рамках геометрической гравитации, без использования понятия силового гравитационного поля.
Вернемся к формуле (6), если принять 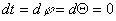 , то это будет вычислением соотношения расстояний в шварцшильдовской системе и падающей. Тогда
, то это будет вычислением соотношения расстояний в шварцшильдовской системе и падающей. Тогда
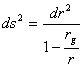
подставив выражение для rg, получим
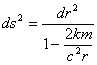
или
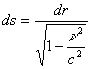 (9)
(9)
где 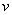 берется из (3).
берется из (3).
Вновь получилась формула преобразования Лоренца [2-(4,5)]. Поэтому (6) можно представить в виде, с учётом (7) и (9)
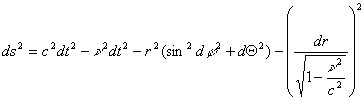
где
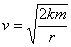
При последовательной подстановке в (6) значения гравитационного радиуса

и второй космической скорости
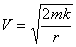
получаем иной вид того же самого решения Шварцшильда
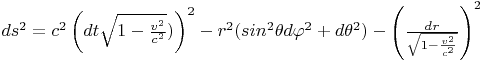
Немедленно видно, что решение Шварцшильда сводится к
комбинации преобразований Лоренца.
И вот здесь появляются различия в результатах, полученных в ОТО и падающей системе. В падающей системе расстояние по вертикали, измеренное по времени распространения света сверху вниз, не совпадает с расстоянием между теми же точками в галилеевой системе при распространении света снизу вверх, а именно
сверху вниз 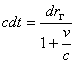 или
или 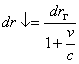
снизу вверх 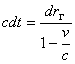 или
или 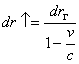
где 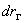 расстояние в галилеевой системе.
расстояние в галилеевой системе.
Этот эффект, конечно же, не мог быть учтен при выводе формулы (6).
Смотрите Расчёт эксперимента по определению
- V -
И еще одна, - четвёртая - система координат, представляющая наибольший интерес в прикладных задачах. Это движение по инерции в области с гравитацией, например, движение планет вокруг Солнца, движение естественного и искусственных спутников в сфере действия тяготения Земли, или просто брошенный камень с ее поверхности. Главное - отсутствие влияния любых сил на движение тела. Траектория этого движения, относительно галилеевой системы, складывается из двух величин: собственного движения тела в падающей системе и движения падающей системы в рассматриваемой точке относительно галилеевой.
Рассмотрим это движение. Положим, что оно происходит в плоскости z = 0. Для i = 0 тело находится в точке A(0,1) с координатами t(0); x(0,1); y(0,1) см. рис.1. Скорость тела относительно падающей системы в точке A:
v(0,1)=AC; vx(0,1)=0C; vy(0,1)=A0. Сдвиг падающей системы в точке A, определяется по формуле (5). Соответственно на рис 1:
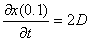 ,
, 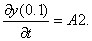
Сделаем шаг в рассмотрении движения: i = 1 тогда t(1) = t(0) + 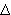 t; тело переместится в точку C(1,0) с координатами
t; тело переместится в точку C(1,0) с координатами
x(1,0) = x(0,1) + vx(0,1) t,
t,
y(1,0) = y(0,1) + vy(0,1) t (11)
t (11)
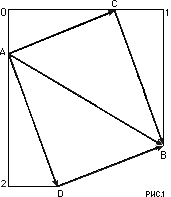
В то же время с учетом сдвига пространства
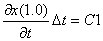 ,
, 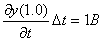 ,
,
тело окажется в точке B(1,1):
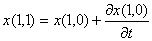 ,
, 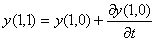 (12)
(12)
За это же время пространство из точки A сдвинется в точку D(0,2) с координатами:
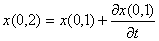 ,
, 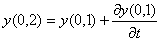 (13)
(13)
Поскольку скорости сдвига падающего пространства в точках A и C различны, то вектор скорости тела AB относительно галилеевой системы за время 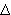 t получит приращение по направлению и величине. Его компоненты будут
t получит приращение по направлению и величине. Его компоненты будут
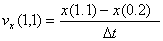 ,
, 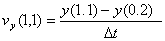 (14)
(14)
Обращаю внимание, что направления векторов сдвига пространства AD и CB пересекаются в центре тяготения.
На основе (11-14) были составлены формулы для программы пошагового вычисления траектории математической точки, движущейся со скоростью света по касательной к Солнцу параллельно оси x в пределах орбиты Земли.
Начальные условия:
y(0,1) = y(-1,0) = y(-1,2) = 7*105 км, радиус Солнца
x(-1,1) = x(-1,2) = (-1.5*108 - 3*105) км,
x(0,1) = -1.5*108 км, радиус орбиты Земли
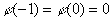 ,
,
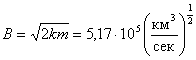 ,
,
c = 3*105 км/сек, скорость света
 t = 1 сек .
t = 1 сек .
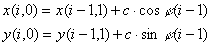
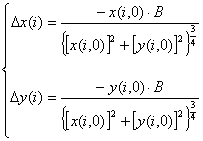
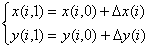 (15)
(15)
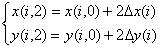
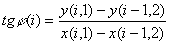
Эти формулы были положены в основу алгоритма и программы 1 (или ftp://rabbit.spider.ru/pub/article1/ekg1.pas), выполненных Панфёровым Е.Е. sad@pisem.net, результаты ее следующие:
отклонение траектории при прохождении орбиты Земли составило 4.2*10-6 рад;
пересечение орбиты Земли произошло на 0.13 мсек позже, чем без гравитации.
При прохождении ближайшей точки к Солнцу, то есть x=0 имелись результаты:
отклонение траектории 2*10-3 рад;
пересечение произошло на 0,23 сек раньше, чем без гравитации.
Сама траектория приведена на рис. 2:
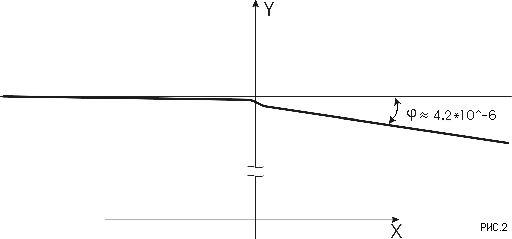
Видно, что она имеет точку перегиба .
Формулы (15) используются как основа для определения траектории луча света, проходящего вблизи Солнца. Поскольку распространение света подчиняется принципу Гюйгенса - см. например [3-236], были использованы два луча, разделенные расстоянием 100 км. Каждый шаг содержит следующие составляющие:
1. Определение точек x1(i,0), y1(i,0) для первого луча и x2(i,0), y2(i,0) - для второго, в соответствии с (15) -кроме вычисления тангенса фи.
.
2. Вычисление угла распространения лучей света для следующего шага:
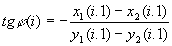
На основании приведенных формул Панфёровым Е.Е. была составлена программа 2 (или ftp://rabbit.spider.ru/pub/article1/ekg2.pas). Анализ результатов, полученных на основе этой программы, можно разделить на несколько пунктов.
1. Траектория светового луча представлена на рис. 3. На начальном участке до x = 4,73*106 км отклонение от прямой увеличивается до 94 км, по мере приближения к перигелию уменьшается до 74 км, и после его прохождения резко увеличивается, достигая 1143 км к пересечению орбиты Земли. Таким образом, вблизи перигелия траектория светового луча удаляется от центра гравитации.
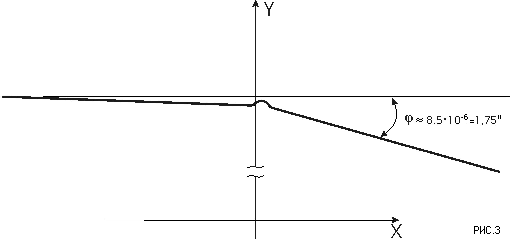
2. Направление распространения светового луча не совпадает с его траекторией - это результат сдвига пространства к центру. То, что геодезическая не совпадает с траекторией луча света, упоминается в [3-218]. На рис. 4 приведено поведение угла распространения луча света: на начальном участке направление распространения луча отклоняется от Солнца, достигая 2*10-3 рад, и после прохождения Солнца он также остается положительным некоторое количество шагов. К пересечению орбиты Земли угол составляет -8.47*10-6 рад = -1.75'' .
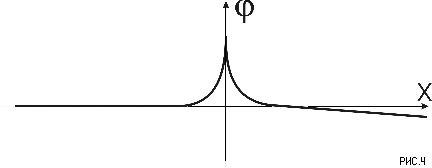
3. Эффект опережения и запаздывания распространения.
Опыт И. Шапиро.
( Irvin I. S h a p i r o )
При приближении луча к
Солнцу его скорость складывается со скоростью смещения падающей системы, и он
достигает орбиты Венеры раньше, нежели луч света в отсутствии тяготения, и это
опережение составляет 0.021380527296 сек.
При удалении от Солнца он движется против
смещения падающей системы, и скорость удаления будет меньше скорости света в
галилеевой системе.
При распространении луча света от орбиты Венеры к орбите Земли задержка составляет 0.021184152373сек.
Итоговое запаздывание составит
0.021380527296-0.021184152373 = 0.000196374923 = 1.963E-4 = 1.963*10-4.
В [8-775] эта
задержка составляет 2*10-4.
Расчёт полностью приведён в http://gek47.narod.ru/a/Shapiro.htm
- VI -
Приведенные расчёты показывают, что теоретические значения гравитационных эффектов, основанные на идее подвижной метрики пространства, совпадают или близки значениям, полученным посредством опыта. Однако ценность этого подхода не в том, что он позволяет легко и точно рассчитать гравитационные эффекты - это уже было сделано в традиционной теории гравитации в рамках ОТО. Ценность данного подхода заключается в ином взгляде на природу гравитации. Здесь вообще нет понятия гравитационного поля. Формой существования гравитации является смещение падающей системы координат. Все эффекты гравитации можно объяснить с единой позиции динамичной метрики. Таких эффектов и следствий теории гравитации в рамках ОТО я насчитал более десятка. В данной работе не ставилась цель объяснить все эффекты, коснусь только нескольких.
Равенство инертной и гравитационной масс. Этот эффект как-то даже неудобно называть эффектом, поскольку именно это равенство является источником основополагающего принципа эквивалентности Эйнштейна и вытекающей из него идее динамичной метрики. Как результат - в падающем пространстве нет вообще такого понятия, как гравитационная масса. Есть только инертная масса, и становится ясно, почему. А именно, тело на поверхности Земли увлекается падающим пространством вниз, этому препятствуют электрические силы отталкивания земной поверхности. Значит, поверхность Земли ускоряет это тело относительно падающего пространства, а там, где есть ускорение, - есть инертная масса. Очень отдаленную аналогию из обыденной жизни можно поставить в соответствие этому явлению, - например, сильный ветер, прижавший незадачливого прохожего к решетке забора. Или частицы мусора, прижатые потоком воды к фильтрующей сетке водоспуска речной плотины. Для лягушки, случайно попавшей на этот мусор, то, что мы называем тяготением для нас, будет направлено перпендикулярно к сетке.
Понятия "гравитационного замедления времени" и "гравитационного сдвига частоты" также не становятся необходимыми. Для понимания этих явлений достаточно аппарата СТО, как, впрочем, и для понимания механизма решения Шварцшильда - это рассмотрено в разделе IV. Не могу не коснуться ещё одного точного решения уравнений Эйнштейна - решения Керра. Возникающая в этом решении метрика Лензе - Тирринга находит своё наглядное истолкование во вращающемся вихре пространства. Для объяснения имеющегося "явления увлечения" не надо прибегать к математике - и так всё наглядно. Каждый из нас не один раз смотрел на воронку в ванне при спуске воды.
Гравитационные волны. Гравитационная метрика пространства в точке характеризуется двумя переменными: направлением и величиной скорости перемещения. Изменение направления смещения пространства является поперечной гравитационной волной, изменение величины смещения - продольной волной.
Хочу предостеречь от отождествления падающего пространства со стоком идеальной жидкости (например, "эфира") в отверстие на дне емкости (или в "чёрную дыру"). Поле скоростей упомянутой жидкости определяется выражением, напоминающее (4), поэтому не все так просто с этой гравитационной метрикой пространства-времени.
Октябрь 1998- май 1999, август 2001- апрель 2002.
Текст переработан октябрь-ноябрь 2002г.
Дополнительно: Расчёт опыта Шапиро
Литература.
1.А.А.Логунов Теория классического Г.П. УФН 1995г. №2 (Т.165) стр 187
2.Л.Д. Ландау и Е.М.Лившиц Теоретическая физика Т II Теория поля. (М.: Наука. 1988 г.)
3. В.Паули Теория относительности. ( М.: Наука,1983 г.)
4.А.Эйнштейн Собрание научных трудов Т.2(1921-1955) М.,НАУКА,1966г.
5. Э.Шмутцер Теория относительности. (М.: МИР,1981 г.)
6.8.Ю.С.Владимиров,Н.В.Мицкевич, Я.Хорски Пространство, время, гравитация. М., Наука, 1984г
7.А.Л.Зельманов Хронометрические инварианты и сопутствующие координаты в общей теории относительности. ДАН СССР Т.107, N6 стр815 (1956 г).
8.Физический энциклопедический словарь. (М.: Советская энциклопедия,1983 г.)
GRAVITATION METRIC
Gribanovskij Eugene Konstantinovich.
The physical process corresponding to the idea of a curvature of Einstein‘s space - time geometry is offered for the explanation of Gravitation. The production of basic results has become possible due to consecutive application of the equivalence principle of Einstein leading to the concept of the dynamical metrics. Four allocated systems of coordinates of central - symmetric area of gravitation are considered. There formulas of transition between them are given. The physical meaning of Schwarzchild`s solution has accomplished. Results of Pound-Rebky`s experiment were reconsidered. Also the experiment of trajectory of a light beam deviation of the Sun without attraction of the concept of Gravitational Field is made. The effect of a light ray’s deviation from the center of gravitation close to perihelion is disclosed.
Gribanovskiy Evgeniy Konstantinovich
e-mail: 
На главную

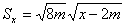 (1)
(1) 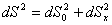 (2)
(2)
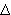 t эта точка переместится на расстояние
t эта точка переместится на расстояние 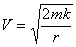 (3)
(3) 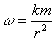 (4)
(4)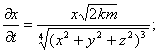
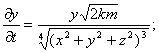
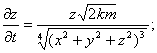 (5)
(5)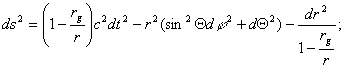 (6)
(6)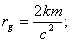
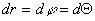 =0,
=0,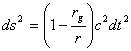
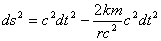 или
или 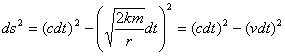 (7)
(7)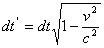 где
где 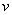 берется из (3)
берется из (3)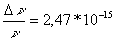 [5-(3.29)]
[5-(3.29)]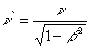 где
где 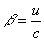 , u - скорость.
, u - скорость.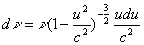 или
или 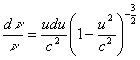 (8)
(8)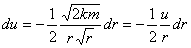
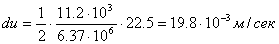
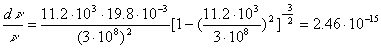
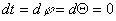 , то это будет вычислением соотношения расстояний в шварцшильдовской системе и падающей. Тогда
, то это будет вычислением соотношения расстояний в шварцшильдовской системе и падающей. Тогда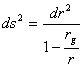
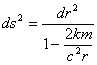
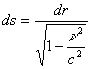 (9)
(9)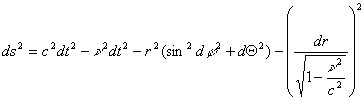
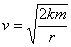

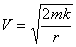
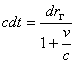 или
или 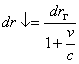
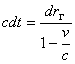 или
или 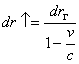
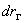 расстояние в галилеевой системе.
расстояние в галилеевой системе.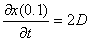 ,
, 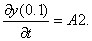

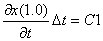 ,
, 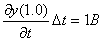 ,
,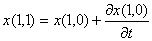 ,
, 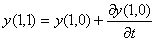 (12)
(12)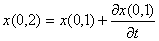 ,
, 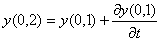 (13)
(13)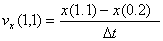 ,
, 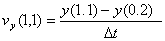 (14)
(14)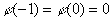 ,
,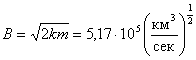 ,
,
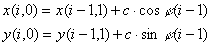
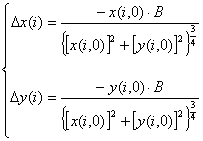
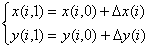 (15)
(15)