Для начала сообщу сразу: этот расчёт проведён в рамках традиционной ОТО, и этот результат правилен для
НЕПОДВИЖНОЙ
относительно центра тяготения системе отсчёта.
Относительно падающей системы скорость изменяется от нуля в удалении до скорости света, соответственно имеется сокращение масштаба в соответствии с формулой Лоренца, и накопление этого сокращения и рассчитано здесь.

Так какое расстояние до чёрной дыры (далее-ЧД.)?

Напомню формулу для соотношения расстояний в галилеевой системе и «искривлённой» из решения Шварцшильда. (Ландавшиц, Т2 100.14)

                                                                         (1)

Приведём её к виду                                                                                      (2)

Или                                                                                             (3)

 

 

 

 

 

Возъмём интеграл от этой функции, принимая верхний предел интегрирования переменным.

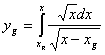         (пределы от x_g до x )                      (4)

 

Смотрим Двайта Г.Б., Таблицы интегралов…стр 33 формула 195.04

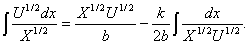                                           (5)

 

где       X = (a + bx)  U = (f + gx),  k = (ag - bf).  

 

В нашем случае       a = -x_g             b = 1,  f = 0,   g = 1,  k = -x_gg – 1*f = -x_g    [bg > 0]

 

В свою очередь, 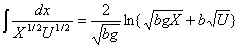при     [bg > 0]          (6)

 

Тогда (5) с учётом (6) будет:

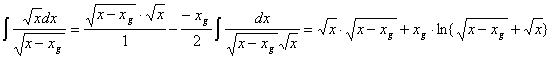
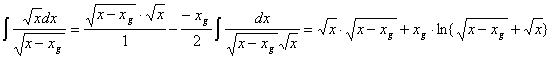                        (7)      

Подставляя в (4) получим:

 

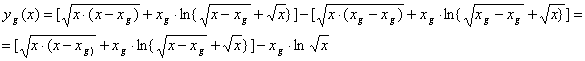            (8)

 

открывая скобки и сворачивая сумму логарифмов получим

 

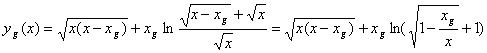
                                       (9)

 

Обдумаем полученное. Первое предложение в начале страницы: Так какое расстояние до чёрной дыры?

Получилось.

А чему равно увеличение расстояния по сравнению с тем же путём, только без гравитации? Из (9) надо вычесть текущее х. С учётом того, что интегрирование производили от x=x_g

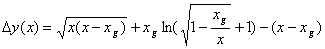
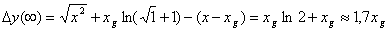                                                         (10)

 

устремляя х к бесконечности, получим

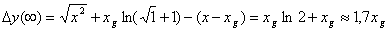
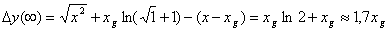                                            (11)

 

Надо же, как этот результат отличается от результатов, если за исходную формулу взять решение Шварцшильда не из Ландавшица, а из Паули, стр 233.

В конечном итоге, если провести с формулой для решения Шварцшильда из Паули те же преобразования, что проделаны здесь, получится

 

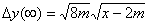
, а это сильно отличается от (11).

Здесь, чем больше x, тем больше разница между метриками.

 

Удивительно, как ошибочная формула в Паули привела меня к мысли, что не всё в порядке в ОТО в целом, и попытка пересмотра всего здания Теории гравитации в рамках ОТО, беря за основу только Принцип эквивалентности, увенчалась    концепцией подвижной метрики.

На главную